Research interests
Research Interests
Mathematical and statistical methodology for cellular biology
How does a cell decide whether to duplicate or die? How and when an embryonic stem cell turn to muscle, blood, neural or another type of cell? How and why some proteins exhibit a roughly 24-hour rhythmic behaviour and what are the consequences when this rhythm is disrupted? How immune responses are triggered and why does this go wrong sometimes?
These are only a few questions that scientists try to solve for a long time now. And while progress has been made, especially during the last decades due to the major biotechnological advances, there are still significant gaps to our knowledge. Filling some of those gaps will not only satisfy our natural feeling of curiosity but will lead to the development of better therapies and prevention strategies for some of the most serious illnesses.
An important part of developing our understanding is played by developing appropriate mathematical and statistical methodology to model, predict, simulate, analyse, design experiments and infer the underlying processes in the living cell using the current experimental and theoretical evidence.
Examples of work in this area are provided below.

Biochemical reaction networks describe the dynamic interactions between sets of molecules (e.g. genes, RNAs, proteins, metabolites) that enable communication of signals, regulation of gene expression, and ultimately every function and malfunction in the life of a cell. The recent experiments, which allow us to observe cells and molecules in real time, reveal that these reaction networks are very noisy. The development of models and algorithms that can simulate and analyse these networks is useful for example in analysing their sensitivities, and in designing experiments. The dynamics of these networks are often modelled as stochastic processes (Markov jump processes), and/or stochastic differential equations.
We have recently developed a fast and accurate stochastic simulation algorithm for oscillating biological networks...More
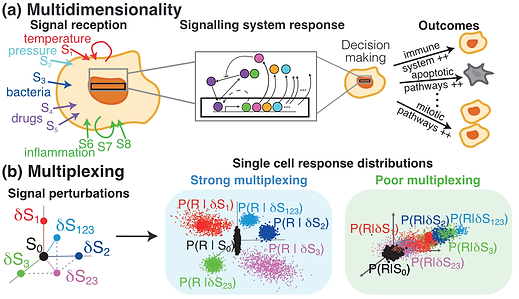
The process by which a cell senses signals from its environment, communicates these signals to molecules within it and take the appropriate actions in response to the signal is extremely important. Signalling errors are associated with many diseases, but on the positive side identification of the key components of this information flow offers opportunities for developing therapeutic treatments. A key question is how this information flow works in a noisy environment of complex interactions where multiple signals are received simultaneously. The process can be understood as follows: the cell is a hypothesis tester which for a given signal decides whether to take one action or the other (e.g. die or multiply) based on the state of some of its key molecules. This approach allows us to develop a mathematical methodology using hypothesis testing, discriminant analysis and information theory and geometry that can help us to better understand cellular signalling, and generate hypotheses to be tested in the lab. Recent work involves measuring the capacity of a signalling system to distinguish multidimensional signals using gene expression data and stochastic modelling of the system dynamics. I currently work with collaborators at the Universities of Warwick (David Rand) and Manchester (Mike White and Pawel Pasczek) on measuring information transduction using single cell RNA sequencing and fluorescent imaging data. I also collaborate in measuring information in cell populations dynamical patterns.


Transcription is thought to be the most important part of the process from which proteins are created from their corresponding genes. This is because transcription is heavily regulated by proteins called transcription factors. Identifying the proteins that regulate, e.g. activate or repress, important genes may allow us to understand transcription and particularly control in disease. Various high-throughput technology is available to observe gene expression under multiple experimental conditions. It is a great statistical and computational challenge to handle, analyse and make inference from such data. We have previously developed a Bayesian statistical methodology for: (i) inferring the switch/jump times of activation or repression of a gene from mRNA or protein expression data (ii) inferring transcriptional regulation mechanisms from multiple dynamic experiments using a Reversible Jump Markov Chain Monte Carlo method, (iii) Bayesian inference for the parameters of stochastic oscillatory systems (see Kalman Filter on the figure). Current work of the group involves the analysis of single cell gene expression data under multple experimental conditions.
Publications
See Google Scholar page

